Transformers
Seq2Seq에서 RNN을 아예 빼버리고 attention으로 구성해보면 어떨까? → Transformer의 구조 현재는 seq2seq + attention에서는 하나의 벡터로…
2025/04/27
Jinsoolve.
성# Language Model(LM)이란?
언어 모델이라는 건, 사실 다음에 올 단어를 확률로 예측하는 것이다.
이러한 언어 모델들을 어떻게 발전시켜왔는 지 살펴보자.
이미 이전 포스트에서 자세히 살펴보았던 내용이다.
이전 n-1개의 단어들을 보고 다음 단어를 예측하는 언어모델이다.
이제 count함수로 확률을 계산하게 된다.

참고로, 저 순서의 조합대로 있어야 세는 거다.
그러다보니 n이 커질수록 해당 조합이 없을 가능성이 점점 높아진다.
그러다보니 다음과 같은 문제가 생긴다.
혼잡도 인데 cross-entropy loss를 exponential 해버린 것과 동일한 의미이다.
loss와 마찬가지로 ppl이 적을수록 좋다.
n-gram 언어모델이 sparsity(말이 되는 말을 0으로 만들어 버림)와 storage(n-gram 순열들 모두 저장해야 함) 문제가 있었기 때문에 신경망 모델로 해결하고자 했다.
fixed-window 크기만큼의 단어를 확인해서 학습하는 방식이다.

각 단어에 대해서 신경망을 통해 학습한다. (사실, binary logistic regression unit 들을 여러 개 쌓아올린 것과 같다.)
W와 U에 각 단어의 의미를 일반화시켜 저장하기 때문에 sparsity 문제도 해결되고, 마찬가지의 이유로 n-gram을 저장할 필요가 없으니 저장 메모리 문제도 해결된다.
윈도우가 너무 작아도 문제이고 그렇다고 키우면 W가 너무 커진다. 그래서 긴 문맥은 이 fixed window로는 감당이 안 되어 버린다.
그리고 결정적으로 각 단어가 위치마다 다른 가중치를 사용해서 같은 단어인데 위치에 따라 다른 의미라고 받아들여진다. → No symmetry
아이디어: 같은 파라미터 W를 반복해서 적용시키면 해결되지 않을까? 라는 아이디어로 해결하고자 함.
그래서 나온 것이 RNN이다.

매번 같은 , 를 사용하고 이전 은닉층의 값을 이용해 현재 은닉층의 값을 계산하는 방식이다.
비선형성을 위해 각 은닉층의 결과에 를 추가해 준다. 그리고 마지막 결과로는 를 해서 확률로 결과를 내보내는 형식이다.
긴 문장도 처리가 가능해진다.
같은 파라미터를 반복해서 사용하므로 메모리가 절약된다.
또한 같은 파라미터를 사용해서 symmetry 를 가질 수 있게 되었다.
그러나 매번 모든 step을 다 계산해줘야 하므로 느리다.
또한 너무 많은 step들이 지나면 해당 정보를 잃어버려서 기억할 수 없게 된다.
→ 해당 부분들은 뒤에서 좀 더 자세히 다뤄보자.

즉, t번 째 은닉층의 손실값에 대한 Gradient (로 편미분한 Gradient이다) 를 계산하려면 ~ r과 현재 층 의 gradient를 모두 더해줘야 한다.
왜냐하면 를 반복해서 사용하기 떄문에 가 매 은닉층마다 영향을 끼치기 때문에 모든 은닉층의 Gradient들을 더해줘야 한다.
근데 바로 여기서 Vanishing Gradient와 Exploding Gradient 문제가 발생한다.

에서 Gradient를 계산할 때, 와 을 모두 더해줘야 하는데(물론 2,3 도 더해줘야 하는데 생략하자), 에 비해 은 을 더 곱해줘야 하는데 이 값들이 만약 1보다 작다면 당연히 값이 줄어들 것��이다.
즉, 최근 은닉층에 비해 옛날 은닉층의 값이 작아져서 그만큼 예전에 했던 말을 기억하지 못 하게 된다.
그러다보니 이 vanishing gradient 문제로 인해 오래 전 말을 기억하지 못하게 된다.

반대로 1보다 큰 값을 여러 번 곱해서 값이 너무 커지게 되면, 업데이트를 할 때 한 번에 너무 큰 step을 가게 된다.

이런 식으로 목표를 자꾸 지나쳐 버리게 된다는 의미다.
그래도 이건 Gradient Clipping으로 어느 정도 완화가 가능하다.

Gradient가 threshold보다 커지면 threshold로 줄이는 방식으로 해결이 가능하다
Seq2Seq에서 RNN을 아예 빼버리고 attention으로 구성해보면 어떨까? → Transformer의 구조 현재는 seq2seq + attention에서는 하나의 벡터로…
2025/04/27
이전 포스트에서 RNN에서 Vanishing Gradient로 인해 장기 의존성 문제가 있다는 사실을 이야기했다. 이런 Vanishing Gradient를 해결하기 위해 크게…
2025/04/27
기존 RNN의 병목 현상을 해결하기 위해 Attention이 등장했다. Decoder에서 한 단어를 예상할 때, 해당 단어와 특별히 관련되어 있는 Encoder의 특정 단어를…
2025/04/27
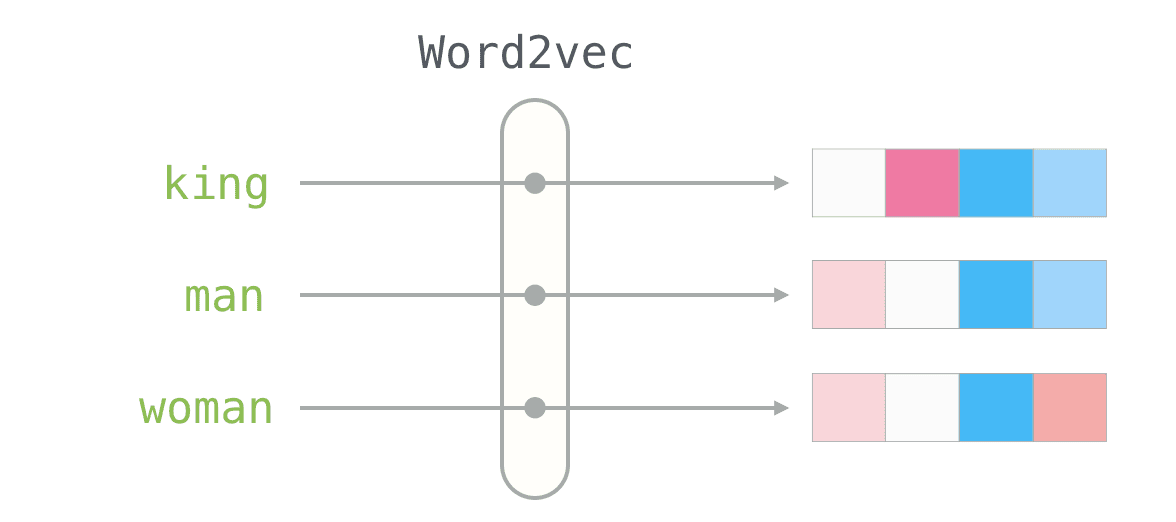
저번에 word vector에 대해서 알아봤는데, 이번에는 word vector의 프레임워크인 Word2Vec에 대해서 좀 더 알아보자. 먼저 Word2Vec이 어떤 식으로…
2025/04/26