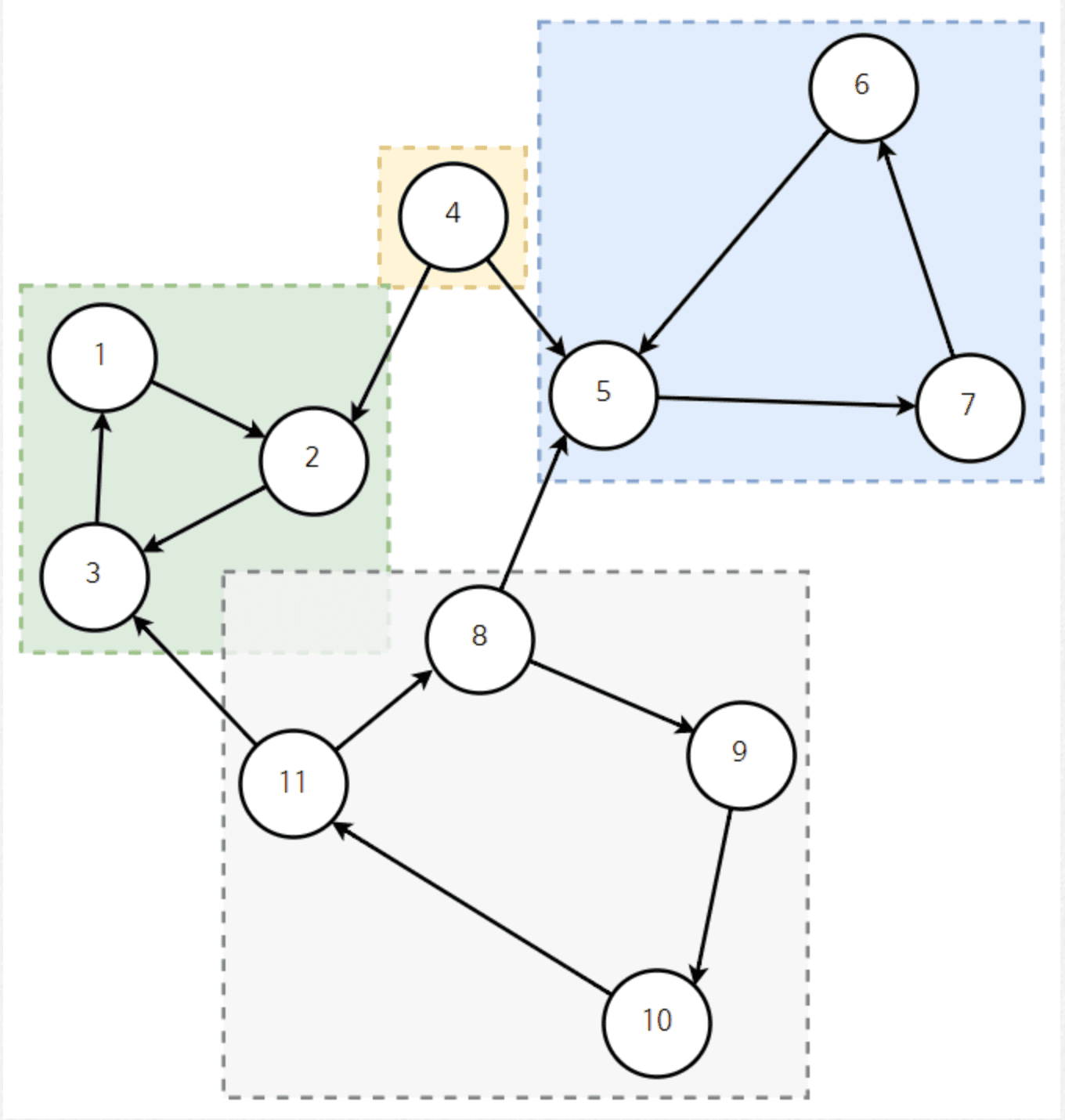
먼저 SCC 즉, 강한 연결 요소가 무엇인지에 대해서 살펴보자.

어떤 컴포넌트가 있는데, 그 컴포넌트 내부의 임의의 노드 u, v가 있다고 하자.
이때, u → v 와 v → u 가 가능한 컴포넌트를 SCC라고 한다.

SCC 알고리즘은 어떤 그래프가 주어졌을 때, 이 그래프 안에 있는 SCC들을 찾아내는 알고리즘이다.

알고리즘#

Tarjan 알고리즘을 사용한다.
(코사라주 알고리즘도 존재한다. 하지만 해당 포스트에서는 타잔 알고리즘만을 다루겠다.)

알고리즘은 다음과 같다.

1. 현재 노드에 방문하면 방문순서를 기록한다.
2. 현재 노드를 스택에 push한다.
3. 초기 parent(가장 빠른 방문순서)는 현재 노드의 방문순서로 초기화한다.
4. 현재 노드의 이웃을 반복하여 방문한다.
   1. 이웃이 아직 방문 전이라면, 재귀적으로 Tarjan 알고리즘을 호출한다.
   2. 이웃을 방문은 했지만 아직 처리 전이라면, parent 방문순서만 업데이트해 준다.
5. parent가 현재 노드라면
   1. stack을 pop하면서 scc에 넣어준다.
   2. 이때 넣어진 노드들은 모두 finish 처리 표시해준다.
6. parent 값을 반환한다.

시각적으로 이해를 돕고 싶으면 동빈나님의 블로그를 참고하면 좋을 듯 하다.

시간복잡도#

시간복잡도는 $O(V+E)$이다.

코드#

cpp
1class SCC {  
2private:  
3    int _id, _scc;  
4    vector<int> id; // id[x] := x번 노드의 방문 순서(고유번호)  
5    stack<int> st;  
6  
7    int dfs(int u) {  
8        id[u] = _id++; // 방문한 순서를 의미  
9        st.push(u);  
10  
11        int parent = id[u];  
12        for(int v : g[u]) {  
13            if(id[v] == -1) parent = min(parent, dfs(v));  
14            else if(scc[v] == -1) parent = min(parent, id[v]);  
15        }  
16  
17        if(parent == id[u]) {  
18            while(true) {  
19                int t = st.top(); st.pop();  
20                scc[t] = _scc;  
21                sccSize[_scc]++;  
22                if(t == u) break;  
23            }  
24            _scc++;  
25        }  
26  
27        // 가장 먼저 방문한 순서를 반환.  
28        return parent;  
29    }  
30  
31public:  
32    int N;  
33  
34    // scc[x] := x번 노드의 scc 번호  
35    // sccSize[scc_x] := scc_x번의 scc의 집합 크기  
36    vector<int> scc, sccSize;  
37  
38    // g := 기존 그래프  
39    // scc_g := scc 끼리의 그래프  
40    vector<vector<int>> g, scc_g;  
41  
42    SCC(int _N) : N(_N), _id(1), _scc(1), id(N+1, -1), scc(N+1, -1), sccSize(N+1,0), g(N+1) {}  
43  
44    void add_edge(int u, int v) { g[u].emplace_back(v); }  
45    void find_scc() {  
46        for(int i=1; i<=N; i++)  
47            if(id[i] == -1) dfs(i);  
48        scc_g.resize(_scc);  
49        for(int u=1; u<=N; u++) {  
50            for(int v : g[u]) {  
51                if(scc[u] != scc[v]) scc_g[scc[u]].emplace_back(scc[v]);  
52            }  
53        }  
54    }  
55};

참고#

• https://blog.naver.com/ndb796/221236952158
• https://programing-note.tistory.com/entry/타잔Tarjan-알고리즘